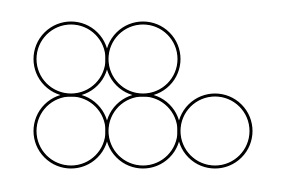Topology – Page 2

Real MATHEMATICS – Strange Worlds #12

“More to this than meets the eye…”

I will be using a real life example in order to explain Mandelbrot’s answer to the coastline paradox.

Maps of Norway and USA are as shown below:

It is clear to the naked eye that total coastline of USA is enormous comparing to Norway’s coastline. Nevertheless there is more to this than meets the eyes. Norway’s coastline is a lot longer than USA’s:

USA: 19.924 km

Norway: 25.148 km

There are more than 5000 km between the coastlines which is a really surprising result. But when you zoom into the maps it is easy to see that Norway’s coastline is way more irregular than USA’s. In other words Norway’s coastline has more roughness. Mandelbrot expresses this in his fractal geometry as follows: Norway coastline has a bigger fractal dimension than USA coastline.

But this doesn’t necessarily mean that a bigger fractal dimension has more length. Length and fractal dimension are incomparable.

Measuring Device

In the coastline paradox we learned that one decreases the length of his/her measuring device, then length of the coastline will increase. This information brings an important question with itself: How did they decide the length of the measuring device for Norway-USA comparison?

This is where fractal dimension works perfectly: Finding the appropriate length for the measuring device.

Q: This is all very well how can a coastline length be measured exactly?

Unfortunately it can’t be done. Today, none of the coastline or border lengths are 100% accurate. Although we are certain about one thing: We can make comparisons between coastlines and borders with the help of fractal dimension. In short, today we are able to compare two coastlines or borders even though we are not sure about their exact length.

Box Counting

Finding fractal dimension is easier than you’d think. All you need to do is to count boxes and know how to use a calculator.

Let’s say I want to calculate the fractal dimension of the following shape:

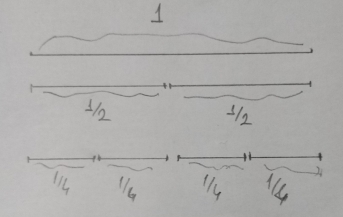
Assume that this shape is inside a unit square. First I divide the square into little squares with side length ¼ units. Then I count the number of boxes which the shape passes through:

This shape passes through exactly 14 squares.

Up next, I divided the unit square into even smaller squares which have side length 1/8 units. And again I count the number of boxes which the shape passes through:

This time the shape passes through 32 squares.

Then I use a calculator. In order to find the fractal dimension of the shape, I must find the logarithms of the number of boxes (32/14) and length of the squares ({1/8}/{1/4}). Then I must divide them multiply the answer with -1.

This random shape I drew on my notebook has around 1,19 fractal dimension.

One wonders…

Calculate the fractal dimension of the following shape:

M. Serkan Kalaycıoğlu

Real Mathematics – Strange Worlds #11

Fractional Dimension

When you try to measure the length of a coastline, your finding will increase as your measuring device decreases. It means that there is a proportion between these magnitudes. This is why it is possible to find different (even infinite) lengths for a random coastline.

Mathematician Mandelbrot named this proportion as “fractal dimension”.

In the Euclidean geometry a dot has 0, a line has 1, a plane has 2 and a cube has 3 dimensions. But, in the nature shapes of objects are not regular as shown in the Euclidean geometry. In the early 20^th century a mathematician named Felix Hausdorff discovered that some shapes have non-integer dimensions. Later on we started calling this non-integer dimension idea as Hausdorff-Besicovitch dimension. This idea was basis for fractal geometry’s development.

In the previous article I showed how one can calculate dimension of a shape in the Euclidean geometry. Same formula can be used in order to calculate objects that don’t have regular shapes. For that, I will be talking about a couple special fractals.

Snowflake

Swedish mathematician Helge von Koch created a geometrical shaped named after him: Koch snowflake.

To create a Koch snowflake, one can start drawing a straight line. Then that line should be divided into thirds as the middle part gets erased:

Draw sides of an equilateral triangle above the removed segment: (In other words, add a peak where there is a gap.)

Continue the same process forever and you will get Koch fractal:

Here are the segments and all of Koch snowflake:

Now let’s use the dimension formula to the Koch snowflake. We only need the number of parts and their lengths in each step of the construction of the Koch snowflake.

In the first step, we had a straight line that was divided into 1/3s:

In the second step we ended up with 4 of those 1/3s:

If we examine each step of the Koch snowflake we will end up with 4 parts that have 1/3 lengths. Therefore fractal dimension of Koch snowflake (which I call d) can be found as follows:

(1/3)^d = 4

d ≈ 1,26.

Koch Curve

Let’s try a variant of the Koch snowflake, which we call Koch curve. This time we will draw sides of a square instead of an equilateral triangle.

So, we will start with a straight line that is divided into thirds. Then we will remove the middle part and draw sides of a square that has no bottom line:

Next few stages of the Koch curve will look like the following:

Here we see that in each step, we end up with 5 parts that have length 1/3:

Apply this to the dimension formula and this fractal’s dimension will be as follows:

(1/3)^d = 5

d ≈ 1,4649.

What does this difference in dimensions mean?

Between the curve and the snowflake, curve has more roughness and it takes up more area than the snowflake. Hence one can conclude that higher dimension means more roughness and more area for Koch fractals:

To be continued…

One wonders…

Another handmade fractal is Sierpinski triangle. This famous fractal was first discovered more than 100 years ago and named after a mathematician named Waclaw Sierpinski.

To construct Sierpinski triangle, one must start with an equilateral triangle:

Then mark middle of each side and connect those points to form a new triangle:

At this point, there are four smaller versions of the original triangle. Cut the middle one out and you will have three equilateral triangles that have half of the side lengths of the original triangle:

Repeat the steps forever and you will get Sierpinski triangle:

Show that Sierpinski triangle is a fractal.
Calculate the dimension of the Sierpinski triangle and compare your result with Koch snowflake.

M. Serkan Kalaycıoğlu

Real Mathematics – Strange Worlds #10

Tearing Papers Up

Use a stationery knife and cut an A4 paper. You will end up with pieces that have smooth sides. Hence you can use Euclidean geometry and its properties in order to find the perimeters of those pieces of papers:

However, when you tear a paper up using nothing but your hands you will be getting pieces that have rough sides as follows:

If you pay enough attention you will that the paper on the right looks just like map of an island.

In the previous article I used properties of Euclidean geometry to measure the length of a coastline and found infinity as an answer. Since those two torn papers look like an island or a border of a country, perimeters of those pieces of papers will also tend to infinity. This is indeed a paradox.

This paradox shows that Euclidean geometry is not useful when it comes to measure things/shapes that have roughness.

Birth of Fractals

“Clouds are not spheres, mountains are not cones, and coastlines are not circles…”

Benoit B. Mandelbrot

There are only shapes consist of dots, lines, curves and such in Euclidean geometry. On the other hand shapes of some natural phenomena can’t be described with Euclidean geometry. They have complex and irregular (rough) shapes. This is where we need a new kind of geometry.

In 1967 mathematician Benoit Mandelbrot (1924-2010) published a short article with the title “How long is the coast of Britain?” where he gave an ingenious explanation to coastline paradox. Furthermore, this article is accepted as the birth of a brand new mathematics branch: Fractal geometry.

The word fractal comes from “fractus” which means broken and/or fractured in Latin. There is still no official definition of what a fractal is. One of their most definitive specialties is “self-similarity”. Fractals look the same at different scales. It means, you can take a small extract of a fractal object and it will look the same as the entire object. This is why fractals are self-similar.

Romanesco broccoli has a fractal shape as you zoom in you will see shapes that look the same as the whole broccoli.

Fractals have infinitely long perimeters. Therefore measuring a fractal’s perimeter or area has no meaning whatsoever.

Coastlines are fractals also: As you zoom in on a coastline or a border line, it is possible to see small versions of the whole shape. (Click here for a magnificent example.) This means that if we had a way to measure a fractal’s perimeter, we can solve the coastline paradox.

So the big question is: What can one do to measure a fractal?

Dimension

According to Mandelbrot, it is possible to measure a fractal’s roughness degree; not its perimeter nor its area. Mandelbrot called this degree fractal dimension. He realized that fractals have different dimensions than the shapes we know from Euclidean geometry.

I will be talking about dimensions in Euclidean geometry before moving on to explaining how one can calculate the dimension of a fractal.

In the Euclidean geometry line has 1, plane has 2, space has 3 dimensions and so on. Teachers use specific examples when this is taught in schools. For space, a teacher asks his/her students to observe any corner of a ceiling:

There are 3 different directions one can choose to walk from that corner. While this is a valid example, it only shows what 3 dimensions look like.

Q: How can one calculate the dimension degree of an object/shape?

Line

Let’s draw a straight line and cut it into two halves:

If straight line had length 1, each segment now has length 1/2. And there are 2 segments in total.

Continue cutting every segment into two halves:

Now each segment has length ¼ and there are 4 line segments in total.

At the point a formula breaks out:

(1/Length of the line segments)^{Dimension Degree} = Number of total line segments

Let me call dimension degree as d.

For 4 line segments:

(1/1/4)^d = 4

4^d = 4

d = 1.

This concludes that line has 1 dimension.

Square

Let’s draw a square that has unit side lengths. At first cut each side into two halves:

There will be 4 little replicas of the original square. And each of those replicas has side length ½.

Apply the formula:

(1/1/2)^d = 4

2^d = 4

d = 2.

Let’s continue and divide each side into two halves. There will be 16 new squares:

Each side of these new squares has length ¼. Apply the formula:

(1/1/4)^d = 16

4^d = 16

d = 2.

This means that square has 2 dimensions.

To be continued…

One wonders…

Apply the same method and formula to find the dimension of a cube.

M. Serkan Kalaycıoğlu

Real Mathematics – Strange Worlds #9

Island S

I own a private island near New Zealand. (In my dreams) Unfortunately I put it on the market due to the economical crisis. If I can’t sell my island I will have to use charter flights to Nice instead of using my private jet.

I created an ad on Ebay. But I choose a different approach when I set a price for my island:

“A slightly used island on sale for 100.000 dollars times the coastline length of the island.

Note: Buyer must calculate the length of the coastline.”

Soon enough I got an offer from a potential buyer. Buyer said he calculated the coastline length as follows:

Buyer used three straight lines in order to measure the length of the coastline. He took each line 8 km long which gave 8*3=24 km. Hence his offer was 24*100.000 = 2.400.000 dollars.

I thought my island worth more than that. Hence I asked the buyer to evaluate his bid again. He came up with a new bid:

This time buyer used seven 5-km-long lines: 5*7=35 km. Thus his second offer was 3.500.000 dollars.

Even though new offer is higher, I thought the buyer can do better. This is why I asked the buyer to measure the length of the coastline one more time:

At last buyer used sixteen 3-km-long lines: 3*16=48 km. Therefore buyer’s final last offer was 4.800.000 dollars.

Q: What is the highest bid I can get from a buyer?

Give yourself a second and think about the answer before continuing the article.

Coastline Paradox

As the buyer decreases the length of the ruler, length of the coastline will get bigger. What is the smallest length for the ruler?

1 cm?

1 mm?

1 mm divided by 1 billion?

There isn’t any answer for the smallest length of a ruler; it can be decreased up to a point where it is infinitely small.

Since there is a disproportion between the length of the ruler and the length of the coastline, coastline can have infinity length.

This is a paradox. Because it is a known fact that there isn’t any land on earth which has infinitely long coastline. Although using buyer’s measurement method, one can’t find an upper limit for the coastline of Island S.

Root of the Problem

British mathematician Lewis Fry Richardson (1881-1953) had done a very interesting research in the first part of the 20^th century. He wanted to know what factors would reduce the frequency of wars between any two country. One of the questions he asked was the following:

“Is there any correlation between the probability of war and the shared border length among two neighbor countries?”

Richardson took Spain and Portugal as an example. Therefore he wanted to know the border length between them. Richardson was really surprised when two countries reported their measurements. Even though they measured the same length, there was a difference of 200 km between two values.

This huge difference led Richardson to pursue the topic and he eventually came up with the coastline paradox.

Is there a sensible explanation for this paradox?

To be continued…

One wonders…

How can my island’s coastline be measured if I want to sell my island for more than 6.000.000 dollars?

M. Serkan Kalaycıoğlu

Real Mathematics – Strange Worlds #8

Do you remember the time I was kidnapped by the aliens? I saved my life thanks to Euler’s formula. Today I will show another method for solving that problem for those who don’t like memorizing formulas.

This method is so remarkable; it actually comes from a theorem called “The Remarkable Theorem”. “Theorema Egregium” belongs to one of the two names I often mention in my articles: Gauss. Well, a remarkable theorem would only fit to the Prince of mathematics anyway.

Gauss’ remarkable theorem shows us the degree of the mathematics internalization in our daily lives. I will use an example in order to explain the theorem:

Example: The (Remarkable) Way of Holding Papers

Take an A4 paper, hold it from left side and try to read what is written on the paper. If you don’t apply any kind of force on your paper through your fingers it will stand like the following:

Paper got bent like this because of gravity. This situation is so internalized in our minds; we solve it with a reflex:

Bending the paper into an inward position helps us beat the gravity and get the paper into a more readable position.

Why?

Why do we have to bend the paper in such situation?

Gauss’ Remarkable Theorem: Gauss says that a plane or an object will have the same Gaussian curvature even after it gets bent, twisted, rotated etc.

Let’s calculate Gaussian curvature of the paper while it lies on the floor. To do that we must select a random point A on the paper and draw two perpendicular lines that go through A:

Now let us analyze the curvatures of these two lines. For each line there will be three possibilities:

If the line is straight, it has zero curvature.
If the line is bent outward, it has positive (+) curvature.
If the line is bent inward, it has negative (-) curvature.

Gaussian curvature is calculated with the multiplication of the curvatures of those two lines. A paper sitting on the floor has zero curvature for both lines which means the paper has zero Gaussian curvature:

Holding the Paper

In the end according to the Gauss’ remarkable theorem Gaussian curvature of a paper will always be zero. No matter what we do to a paper its Gaussian curvature will be zero.

Now let’s go back a bit and examine the Gaussian curvature of the paper when I was holding it. At first paper was curved outward. This means that the paper has positive curvature horizontally:

But vertically paper has zero curvature:

Multiplying positive with zero makes zero, which means the paper has zero Gaussian curvature. Gauss’ remarkable theorem holds on.

Next, we will be analyzing the Gaussian curvature of the paper when my hand forced it on an inward position. Vertically inward position means a negative curvature as horizontally paper has zero curvature. Multiplication gives a zero Gaussian curvature for the paper. Gauss’ theorem is indeed remarkable!

Gaussian Curvatures

Zero Gaussian Curvature:
Both horizontally and vertically it has zero curvature.
Positive Gaussian Curvature:
Positive(horizontally) times positive(vertically) makes positive Gaussian curvature.
Negative Gaussian Curvature:
Negative(horizontally) times positive(vertically) makes negative.

Running Away From the Aliens

Now you can solve the puzzle of the aliens without needing of a formula. All you need is to pick a starting point and determine the Gaussian curvature.

20190131_185431 — Left to right: Zero, positive and negative Gaussian-curvatured shapes.

Zero Gaussian curvature means a paper-like, positive means a sphere-like and negative means a saddle-like shape.

One wonders…

The (Remarkable) Way We Hold a Pizza Slice

How do you hold your pizza slice while you are eating it?

Why?

M. Serkan Kalaycıoğlu

Real Mathematics – Strange Worlds #7

Mathematics is tough

Most of the people I meet tell me that they have never been good at mathematics. It is upsetting to hear such thing especially when they come from adults. Because even though they don’t realize it, these adults are having negative effects on kids.

Understanding mathematics is not easy. Doing it is not easy either. And as if these are not enough, kids hear how unnecessary it is to learn mathematics. It is not hard to find memes about the redundancy of trigonometry or algebra. I love memes by the way.

What should a 10-year old think when he/she hears that the thing you can’t do at school is not even useful after school? This student would distance him/herself from not only mathematics but all sciences until the end of time.

Worst thing is that this student (future adult) wouldn’t even have any idea about what he/she lost.

In almost every country there are huge masses who don’t know what mathematics is and how useful it would have been for them.

Perspective

One of the most crucial things one can gain from mathematics is having the ability of perspective. Whenever you are facing with a problem in life it would help you to solve that problem more quickly if you are capable of looking at thing from different angles.

Perspective is not only useful for solving problems. It helps one to understand other people’s feelings, thoughts, and state. Having perspective helps you to become an empathic person.

Actually having perspective relates to a habit. Mathematics can be very handy if you’d like to build a new habit for your mind. Personally I believe topology is cut out for it.

Engineer’s Problem

Points A-A’, B-B’ and C-C’ should be connected.

A-A’: Electric system for the house.

B-B’: Gas system for the house.

C-C’: Water system for the house.

These three connections should not intersect with one another to avoid accidents such as fire. This is when the engineer is needed: Finding the right paths as electric system must be built first.

Engineer knows that there are 3 different paths for A-A’: Between B’-C’, B-C’ and C-B’. But there seems to be a big problem here. When engineer tries to connect any of those lines, it is impossible to connect B-B’ and C-C’.

How can the engineer solve this problem?

Beauty of Topology

Topology is very useful in case you can’t see a solution right away. In this amazing branch of mathematics we are allowed to deform objects. If so, then let us deform the shape of the problem in our imagination.

There would be no problem if B’ and C’ were replaced. This is the point where we’ll be using topology: If whole area of the shape was made of a kind of fluid, points B’ and C’ could be pushed away from their original places. And if we are allowed to push away these points, everything in between would have been pushed as well. This is why the connection between A-A’ would have been deformed as shown below:

You could imagine A-A’ as a string.

This deformed A-A’ path is engineer’s solution to the three connections problems.

Then, if A-A’ connection is done first, B-B’ and C-C’ connections can be done as follows:

One wonders…

In the following picture you will be seeing a famous problem called “three utilities problem”.

Now take a pen and a cup in your hands and try to find a way to connect three utilities to three houses.

M. Serkan Kalaycıoğlu

Real Mathematics – Strange Worlds #6

Morning Ritual

Famous French philosopher Descartes had a rough childhood as he dealt with various illnesses including tuberculosis. His health condition effected his early school life. He was always late for school. After some time Descartes developed a habit of laying in his bed until noon. It is now known that he spent his mornings in bed thinking about life, nature, mathematics and so on. (Yes, Descartes was in fact a brilliant mathematician.)

René_Descartes_i_samtal_med_Sveriges_drottning,_Kristina — Rene Descartes (right) and Queen of Sweden Christina.

This habit of Descartes kept going until he started working for the queen of Sweden. Apparently she wanted to learn mathematics every day at 6 o’clock in the morning. I try to avoid making speculations in these articles, but I wasn’t surprised that Descartes passed away right after he moved to Sweden! (Warning: Pure speculation.)

I feel for Descartes as I have my own morning rituals too. After waking up I need some time until my senses come back to me completely. Hence I keep my breakfasts as short as possible. Cornflakes are ideal for people like me, although I get sick of getting cornflakes every morning. This is why once in a while I take a week off of cornflakes and declare such weeks “toast & coffee” weeks.

Equality

I am not sure when this happened but every move I make is completely automatic during my toast & coffee mornings: Switch the kettle and the toaster on, prepare the bread slices and cheese (some days ham), cut the toast diagonally so that there will be two equal right-angled triangles, finish making the coffee.

Some mornings my involuntary moves during my breakfast preparation cause a huge problem: I can’t cut the right-angled triangles equally. Uneven triangle toasts? That sounds disturbing, doesn’t it?

Pancake Theorem

Assume that there is one pancake and two of you. There is always a single knife-cut that will give two equal pieces of pancake.
In case there are two pancakes with two different flavors, again there will always be a single knife-cut which will give equal pieces of both pancakes.

Pancake theorem is a good example for cutting two equal parts in a 2 dimensional plane. In case we try that in a 3 dimensional plane, another theorem called the ham-sandwich theorem will come to our rescue.

Ham-Sandwich Theorem: Imagine you have a ham sandwich. Mathematics says that it is always possible to slice the sandwich with one cut so that the ham and both slices of bread are each divided into equal halves.

It sounds obvious and simple. However there are deeper meanings inside this theorem. Let’s assume that you are a careless person and you prepared the sandwich haphazardly: Ham is on top of the bread slices. Ham-sandwich theorem says that it doesn’t change anything; there will be such cut that will give us two equal pieces of each ingredient.

Suppose that you prepared your sandwich perfectly but you dropped it on the floor. Now, bread slices and ham are far away from each other. Theorem says that this won’t change anything. Even if the ingredients are far away from each other, there is always a single cut which will give us equal pieces of them.

One wonders…

Sandwich’s ingredients, not even its shape is important. Sounds like topology spirit, huh?!
Imagine you have five equal circles as shown:

Is it possible to have a cut that will result two equal parts of circles?

M. Serkan Kalaycıoğlu

Real Mathematics – Graphs #3

Do I Know You?

Frank Ramsey was tangling with a mathematics problem back in 1928. In the end he realized that he should invent a whole new mathematics branch in order to find a solution to this specific problem. Unfortunately Frank Ramsey died at the age of 27, even before his findings were published. Although he won immortality as this new mathematics branch was named after him: Ramsey Theory.

220px-Frank_Plumpton_Ramsey — Frank Ramsey (1903-1930)

One of the fundamental problems in Ramsey theory: Could one find order inside chaos? (Here, chaos is used as “disorder”.)

Ramsey theory has various applications in different mathematics branches including logic and graph theory. In this article I will be talking about how graph theory emerges with Ramsey theory.

What is needed: Randomly chosen six people.

Existing chaos: Among those six people who is friends or not friends (strangers) with whom. (Being a friend is mutual: Just because you know Sean Connery doesn’t mean that you are friends with him.)

Desired order: Set of three people among the group of six who are friends or not friends with each other.

Let’s draw the graph of these six people in which dots will represent the individuals, straight lines will represent friendship and dashed lines represent being strangers (not friends).

You might wonder where chaos is in this graph. There are over 30.000 possibilities for only six people to be or not be friends with each other. This is an enormous numbers for a very small group and the graph above shows only one possibility.

220px-Rasputin_PA — Rasputin knows everyone…

In our graph a triangle with sides that are straight lines means that three people are friends with each other. That means a triangle with sides that are dashed lines shows that three people are not friends with each other. This is why we have to look for any kind of triangles in the graph. Obviously we see multiple examples of both in our graph: For instance Bill-Rasputin-Lewinsky makes a friendship triangle as Alexandra-Lewinsky-Hürrem makes a not-friends triangle.

Now there is another important question: How can we know that all those over 30.000 possibilities possess either one of these triangles?

Yes

As it is almost impossible to try every single possibility, we have to come up with a simple and short proof.

Take Rasputin in hand: If he was friends with everyone that would mean that he had 5 friendships and 0 not friendships. All the possibilities for Rasputin are shown below:

These possibilities show us that for every individual in the group, there are at least 3 possibilities for being friends or being strangers. So, we can choose either one of them. Assume that Rasputin is friends with 3 people in the group.

At this situation in order to avoid a triangle for friendship with Rasputin, Lewinsky-Hürrem-Alexandra should be strangers with each other.

Thus, those three would provide a triangle with dashed lines: A triangle of strangers.

This proves that every one of those over 30.000 possibilities has at least one three-friend set or one three-stranger set.

If Lewinsky is friends with Hürrem, they make a friendship triangle with Rasputin. Same goes for Hürrem&Alexandra and Lewinsky-Alexandra. Thus it is impossible to avoid triangles.

One wonders…

Try to find out what would happen if we had 5 people in our group.

M. Serkan Kalaycıoğlu

Real Mathematics – Strange Worlds #5

WHERE AM I?

Let’s assume that you have an object shaped like a sphere. Take a pen and draw a starting point on the object. Then, select a direction and move in that direction from your point. When your tour is completed, you’ll be ending up at your starting point in your original direction.

This is an obvious fact which would never change no matter which starting point or direction you choose.

Orientability: Mathematical definition of orientability is really complicated, even for a mathematics graduate. Which is why I will use an example to define it: Imagine that you are travelling to east from Hamburg with a zeppelin. If you continue travelling, and if you are lucky enough to survive, you would eventually end up at Hamburg while your zeppelin faces east. (Please leave you flat-earthers) Actually, it doesn’t matter which direction or city you choose, result will always be the same. If an object or a surface has this specialty, then we say that it has orientability.

It is absurd to think that you finish travelling as a mirror image of your starting state. If you move to the east from a point, you won’t accidently end up at the same point with your direction flipped to west. In other words, you won’t finish taking a tour on a sphere as your mirror image.

Two types of mirror images. Obviously I am talking about the one on the right.

Is it possible to have an object that doesn’t have orientability? Is it possible to go east and when you arrive at your starting point you realize that you are standing upside down?

YES!

Möbius Strip

Cut a rectangle shaped paper. This paper has two faces.

There is no interchanging from one face to another. It means, if you start moving on one face, no matter where or in which direction you started, you won’t end up in the other face. We can call these faces “roads”. So a paper has two different roads.

A paper can have two faces (roads). You can’t go from I to II.

Now glue the ends of this paper together. You will have a cylinder. A cylinder has two faces like a flat paper. It means that a cylinder has two different roads. It is not possible to use one road and end up in the other road. This is why a cylinder has orientability.

Use a transparent paper and make a cylinder. Mark a starting point on your cylinder and move it around your finger until you are at your starting point. You would end up in the same conditions.

Let’s go back: Take your flat rectangle paper and while bringing their ends together twist one end 180 degrees. Mathematicians call this shape a Möbius strip.

While constructing, that 180 degree twist on one end is the only difference between a cylinder and a Möbius strip. But, this difference has absolutely mesmerizing results. First thing to notice is that there is only one face in a Möbius strip. That means a Möbius strip has only one road.

Let’s use a transparent paper again and construct a Möbius strip. Select a starting point and move the strip around your finger. When you end up at your starting point, you’ll see that “up” became “down”, “down” became “up”. In other words, you ended up as your mirror image on a Möbius strip.

Up-right became up-left as if there is a mirror between them.

Then, there is no orientability for Möbius strips. Also, if you make a second tour on it, you would end up at the starting point as your original state.

A little bit of history

It is surprising to learn that Möbius strip was first discovered around 160 years ago. This simple but mysterious shape took its name from the German mathematician August Möbius. Although, Johann Listing, who is another German mathematician, was the first person who published about Möbius strip.

August Möbius (left) and Johann Listing (right).

That is because August Möbius and Johann Listing discovered about Möbius strip independently almost at the same time. After looking through their personal notes we understood that August Möbius discovered the strip 2 months before Listing did. Even though Listing was the first person to use the word “topology”, 2 months gave August Möbius a better mortality.

One wonders…

Construct two Möbius strips. While twisting them, twist one of them to the right and the other one to the left 180 degrees. Do you see any difference?
Construct a cylinder and cut it into its middle in the direction parallel to its longest edge. You will end up with two cylinders which are little replicas of the original cylinder.
Try the same thing on a Möbius strip. What is the result? Why did you have that result?

M. Serkan Kalaycıoğlu

Real Mathematics – Strange Worlds #4

Orange Season

I like using oranges for mathematics because I think they taste awesome. Also, its shape is close to Earth’s shape which I believe is a cool resemblance. Even though I’d love to, I can’t take credit for using orange with examples about Earth. It belongs to a deep and important dispute in the history of science.

17^th century is known as the century when the modern science was born. Giovanni Cassini, an Italian astronomer was born in this century along with so many other important figures. He is famous with discovering Saturn’s rings and its four big moons. In addition, he went into a big dispute with Isaac Newton, who is known as the father of modern physics. I’ll save Newton’s introduction for another article.

Dispute began with Cassini’s measurements which he did with his son. Those measurements led him to a wrong conclusion. He resulted that Earth is elongated at the poles, like a lemon. On the other hand, Newton had explained that Earth is flattened at the poles, like an orange. This was a result Newton reached after his gravitational laws. Unfortunately for Newton, Cassini openly rejected Newton’s gravitation laws which made him adopt his stance even harder after the measurements he had for determining the shape of Earth.

gravity-orange-lemon-small (2) — Newton suggested that Earth’s shape is like an orange as Cassini wrongly claimed that it looks like a lemon.

This dispute continued for almost forty years until French Geodesy Mission (1736-1744) was completed. Measurements and calculations had proven Newton right: Earth was shaped like an orange.

Finding Circumference

Stick two equal-sized straws on an orange.

Direct a flash lamp to one of the straws so that it doesn’t have a shadow.

If the distance between those straws is given, is it possible to calculate the circumference of the orange?

Second-Best of Everything

Eratosthenes was born in the ancient city of Cyrene, at around 3^rd century BC. He is known as the person who discovered (or invented) geography. There is an interesting take from Thomas Hearth (1861-1940) who was an important historian of mathematics specifically on ancient Greek mathematics: “Eratosthenes was great on every subject of science, but he was never ‘the best’ in one area. You may imagine him like an athlete who competes in every branch of Olympics but comes second in those competitions.”

Even though he founded an important science branch like geography, Eratosthenes is known with calculating the circumference of the Earth almost 2200 years ago. And he did it with a surprising accuracy. But how did he manage it?

Eratosthenes realized on a summer day that he had no shadow at noon in Cyrene. Although at the same time when he tried it in Alexandria he saw a shadow. Eratosthenes believed that Earth was round and Sun is too far away from Earth. He also thought of light rays travel as parallel lines which is why he made an experiment that took place in Cyrene and Alexandria. He observed a tall tower’s shadow in Alexandria when there is no shadow in Cyrene. Eratosthenes measured that the shadow of the tower makes a 7,2-degree angle with its bottom. He also had the distance between two cities measured that enabled him to calculate the circumference of the Earth.

A as Cyrene and B as Alexandria.

Eratosthenes used an ancient Greek measurement called “stadium” in his calculation. Since a stadium means something between 154- 215 meters, we are not 100% sure what his calculation was. In the end, his solution and method was good enough to put him into the highlights of the history of science.

Circumference of the Orange

Now that you know Eratosthenes’ method, could you find the circumference of the orange?

Hint: The angle straw makes is 12 degrees and distance between straws is exactly 1 cm.

M. Serkan Kalaycıoğlu